When setting out to determine what cylinder to use for your application, regarding the force, we can work from two different approaches. Either we know the dimensions of the cylinder and we want to determine how much pressure to feed to result in a desired force (or the other way around). Or we want to determine what the dimensions of our cylinder ought to be when we know how much force we want to apply with a given pressure. (Besides the force of the cylinder, we can then look at the speed with which the cylinder moves in and out. This is influenced by the volume as well as the flow that we feed the cylinder. More of the speed of the cylinder in another article: link.)
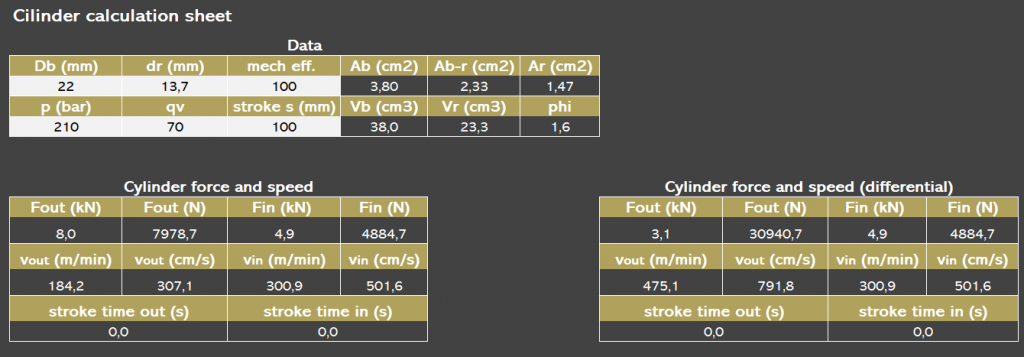
If you do not want the theoretical background and just go on with it, download our cylinder calculation sheet for free!
Theoretical
Force is the result of a pressure over a certain area, thus:
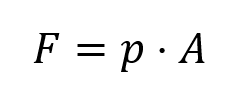
F = force in (N) or (kN)
p = pressure in (Mpa) or (bar)
A = surface area in (mm2) or (cm2)
For convenience purposes I like to calculate the cylinder force in kN with bar and cm2 since the outcome of the calculation is then easier to read.
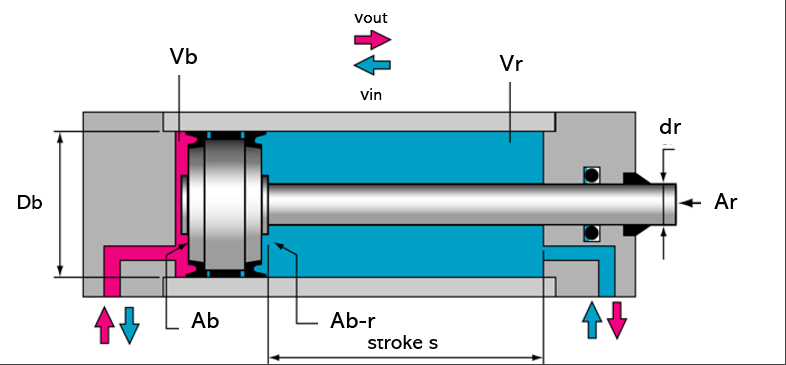
The cylinder has two sides: the bore side and the rod side (with the ring surface area). The rod side can put forth less force than the bore side because of the smaller area, yet the rod will retract faster with the same flow due to the smaller volume. This is the result of the rod filling up a certain area and volume. The ratio between these two sides is called: phi (unitless).
Bore side surface area
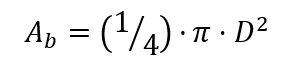
Ab = bore side surface area (mm2) or (cm2)
D = bore diameter (mm) or (cm)
Rod surface area
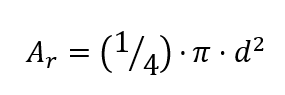
Ar = rod surface area (mm2) or (cm2)
d = rod diameter (mm) or (cm)
To calculate the Ring surface area, we can simply extract one from the other:
Ring surface area
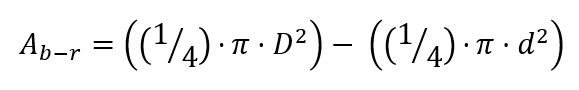
Ab-r = ring surface area (mm2) or (cm2)
D = bore diameter (mm) or (cm)
d = rod diameter (mm) or (cm)
Example 1
Now to calculate the force of the cylinder I shall demonstrate by using an example. In this example the dimensions of the cylinder are known, and we want to calculate the force of the cylinder:
Data:
p = 210 bar
Db= 125 mm
Dr = 90 mm
Requested:
Fin = ?
Fout = ?
Formula:
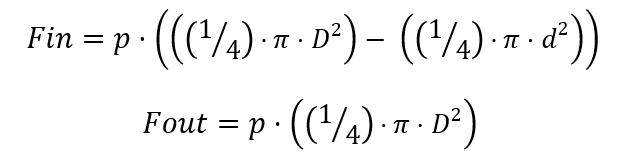
Solution:
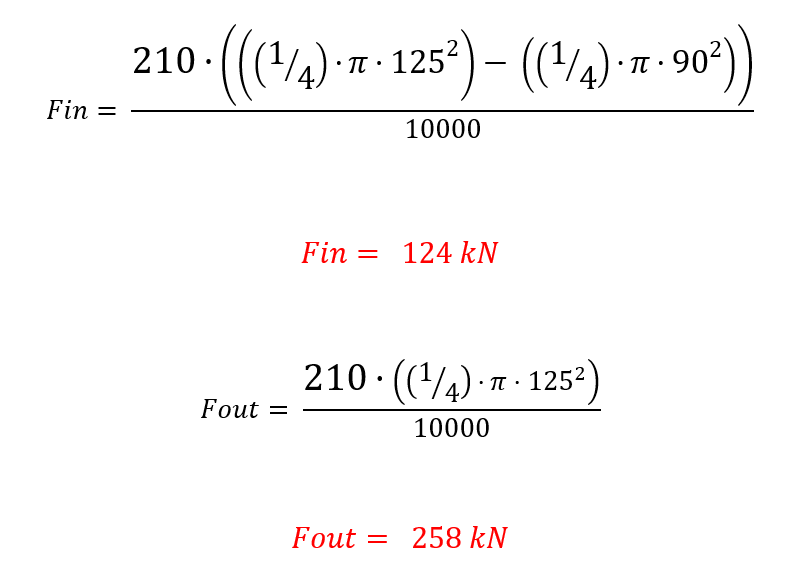
Note: that the solution is divided by 10000, this is to correct for the units we used. This number will be 10 when we calculated everything in cm instead of mm.
In reality, we can’t escape the real efficiency of the system. Therefor we should multiply our result with an efficiency percentage. As a rule of thumb one can use a value of 0.95 (95%).
Example 2
The other way around is a bit more of a fuzz. When we want to calculate the dimension of our cylinder, when we already know what force we want our cylinder to bring forth, we can go about the following way:
Data:
Fout = 8 kN
Fin = 5 kN
p = 210 bar
Requested:
D = ?
d = ?
Formula:
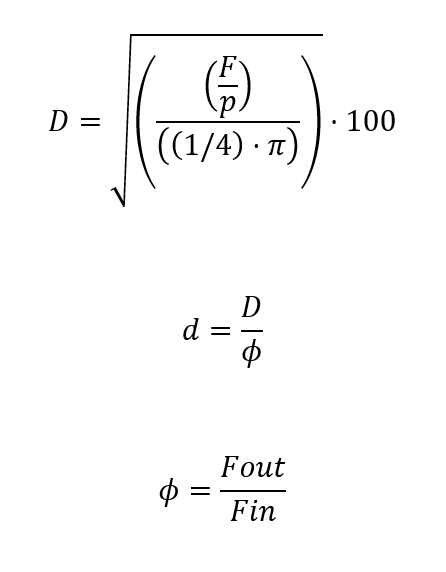
Solution:
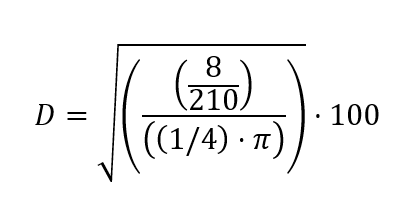
Note: make sure you first take the square root before multiplying by 100.
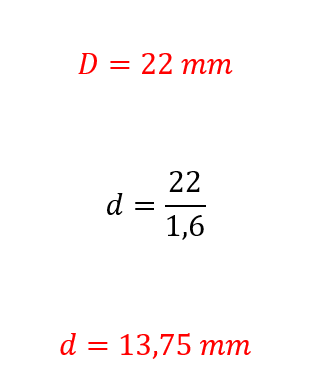
Note: always try to find standard cylinders before configurating your own special one. This is not only more cost efficient, but it also increases the chance that the delivery time is shorter when you order.
Now we have calculated the force of our cylinder we can look at the speed at which we want the cylinder to move in and out. For the speed of the cylinder, see the article: Cylinder speed calculation. (See also for the differential cylinder calculation.)
If the stroke of our cylinder is too long, in comparison to the force we apply, we could kink the cylinder rod. To avoid this issue, we can calculate the kink point of our cylinder. For the kink point calculation of the cylinder, see the article: Cylinder kink point calculation
Download link calculation sheet! Free!

Add a comment